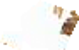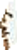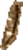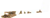P. BM EA 10399Mathematischer Text
Ägypten332 - 30 BCE
•
Parker, R.A., Demotic Mathematical Papyri (Brown Egyptological Studies 7; Providence, R.I., 1972), 53-63 [no. 41-52], pls. 15-18.
•
Website of the British Museum.
Beschriftung
|rto.x+II.1 𓌡:𓂝*𓏤3 𓆱:𓏏*𓏤𓆱:𓏥𓊡𓏭:𓏛 𓇋𓏲𓆑 ⸢𓊢𓂝:𓂻 ...⸣ [...] .
𓇋𓇋𓏲
𓄿1
?. [...
𓇋𓏲𓆑] 𓁹:𓂋*𓏭 𓅓1𓎔1𓊹𓅆 𓍢 𓅓1𓂸:𓏏𓂭𓂭𓀁° 𓇋𓏲𓆑 𓁹:𓂋*𓏭 𓅓1𓎔1𓊹𓅆 𓏼1 𓆷1𓃭𓏤𓀁 𓂋:𓂧@𓂾:°𓂾:°𓍘1 𓆑1
|rto.x+II.2 𓇋𓏲𓆑 𓁹:𓂋*𓏭 𓅓1𓎔1𓊹𓅆 𓏺 𓈖 𓄂:𓏏*𓏤𓄣𓏤𓄹:𓏭2@𓍘1 𓆑1 𓎼𓃭𓉻:𓂝*𓏛𓀁°𓏪 𓈔𓏤°𓈒:𓏥2 𓇋𓏲𓆑 𓄖:𓂻 𓇋𓏲𓏪 𓏎:𓈖 𓅯𓄿 𓆱:𓏏*𓏤𓆱:𓏥𓊡𓏭:𓏛 𓂋1⸢𓈐:𓂻⸣ 𓏌:𓈖𓉐𓏤2
|rto.x+II.3 𓏏:𓄿 𓎼𓃭𓉻:𓂝*𓏛𓀁° 𓅓1𓏲:𓏏:° 𓏪 𓆼𓇋𓇋𓏲𓂷:𓂡 ⸢𓈗𓏤1𓈘:𓈇⸣ 𓂋1 𓏏:𓄿 𓎼𓃭𓉻:𓂝*𓏛𓀁° 𓇋𓏲 𓂷:𓂡1 𓇋1𓐍:𓏭 𓈗𓏤1𓈘:𓈇 ⸢𓂽⸣
|rto.x+II.4 𓇋1𓐍:𓏭 𓅯𓄿 𓍓@𓉐𓏤2 𓅓1𓎔1𓐍:𓂧𓉐𓏤2 𓅯𓄿 𓆱:𓏏*𓏤⸢𓆱:𓏥⸣𓊡𓏭:𓏛 □
𓅯𓄿 𓎼:°𓇋𓇋𓏲𓀾° 𓈖2:
𓁹:𓂋*𓏭𓆑 𓏴:𓏛
|rto.x+II.5 𓇋5:𓎡 𓎝𓎛𓎛3 𓌡:𓂝*𓏤3 𓁷𓏤𓏤1 𓆷1𓃭𓏤𓀁 𓈖 𓄂:𓏏*𓏤𓄣𓏤⸢𓄹:𓏭2@𓍘1⸣ 𓆑1 𓂋1 𓏼1 𓁷𓏤𓏤1 𓆷1𓃭𓏤𓀁 𓂋:𓂧@⸢𓂾:°𓂾:°⸣𓍘1 [𓆑1] ⸢𓂋1 𓏽1⸣
|rto.x+II.6 𓇋5:𓎡 𓂷:𓂡1 𓏏:𓄿𓇋𓇋𓆑 𓊪1:𓈙𓏴:𓂡 𓂋1 𓏻1 𓇋5:𓎡 𓁹:𓂋*𓏭 𓏻1 𓂋1 𓊃2:𓊪1° 𓏻1 𓂋1 𓏽1
|rto.x+II.7 𓇋5:𓎡 𓂷:𓂡1 𓅯𓄿𓇋𓇋𓆑 𓏴 𓆣:𓂋𓏲 𓇋𓏲 𓈖:𓏏*𓏭1𓎟:𓏏 𓁷𓏤𓏤1 𓆷1𓃭𓏤𓀁° 𓐍':𓂋5𓀁 𓌪:𓂡𓍘1 𓅯𓄿𓏲𓏛:𓏥 𓏴 𓈖𓇋𓅓𓏭:𓏛 𓏪 𓏭:𓂢 𓏼1
|rto.x+II.8 𓇋5:𓎡 𓁹:𓂋*𓏭 𓍢 𓂋1 𓊃2:𓊪1° 𓏼1 𓂋𓌥𓏲𓏭:𓏛 𓅯𓄿 𓅓1𓂸:𓏏𓂭𓂭𓀁° 𓅯𓄿 𓆱:𓏏*𓏤𓆱:𓏥𓊡𓏭:𓏛 𓈖:𓏏*𓏭1 𓁹:𓂋*𓏭 𓍢 𓂋1 𓍤 𓅯𓄿 𓍓@𓉐𓏤2 𓅯𓄿 𓆱:𓏏*𓏤⸢𓆱:𓏥𓊡𓏭:𓏛⸣ [𓅯𓄿𓏭1]
|rto.x+II.9 𓅯𓄿 𓎼:𓂋𓇋𓇋𓏲𓀾° 𓈖2:
𓅠𓏭:𓏛 𓅯𓄿 𓍓@𓉐𓏤2 𓉔1':𓈖1𓏤1𓈘:𓈇 𓈖:𓏏*𓏭1 𓈝𓂻:° 𓂋1 𓅯𓄿 𓅓1𓎔1𓊗:𓏻2@ 𓏺 𓁷𓏤𓏤1𓄡:𓏏*𓏤@ 𓏺 𓅓1𓏏1:𓇋𓇋𓏲⸢𓀁°⸣ [𓆑 𓏺]
|rto.x+II.10 𓇋5:𓎡 𓂋:𓐍@ 𓅯𓄿 𓍓@𓉐𓏤2 𓂧:𓏏*𓏤1 𓈖:𓏏*𓏭1 𓈝𓂻:° 𓂋1 𓅯𓄿 𓅓1𓎔1𓅝:𓏏*𓏭𓅆° 𓂋1 𓐀1
|rto.x+II.11 𓇋5:𓎡 𓁹:𓂋*𓏭 𓐀 𓂋1 𓊃2:𓊪1° 𓐀 𓂋1 𓎉𓐂1
|rto.x+II.12 𓇋5:𓎡 𓁹:𓂋*𓏭 𓎉𓐂1 𓂋1 𓊃2:𓊪1° 𓐀 □
𓂋1 𓍤𓎉𓏼1
|rto.x+II.13 𓇋5:𓎡 𓆓:𓂧 𓅯𓄿 𓉔1:𓈖1𓏌 𓂧:𓏏*𓏤1 𓏺 ⸢𓁷𓏤⸣𓏤1𓄡:𓏏*𓏤@ 𓏺 𓅓1𓏏1:𓇋𓇋𓏲𓀁 𓆑1 𓏺
|rto.x+II.14 𓇋5:𓎡 𓆓:𓂧 𓐍':𓂋5𓀁 𓈝𓂻:° 𓉔1:𓈖1[𓏌 𓍤𓎉𓏼1 𓂋1 𓅓1𓎔1] 𓏺 [𓁷𓏤𓏤1𓄡:𓏏*𓏤 𓏺 𓅓1𓏏1:𓇋𓇋𓏲𓀁 𓆑 𓏺]
|rto.x+II.15 [𓇋5:𓎡 𓁹:𓂋*𓏭] 𓍤𓎉[𓏼1] 𓂋1 𓊃2:𓊪1° 𓍤 𓈖:𓏏*𓏭1𓇋𓏲 𓅯𓄿 𓍓@𓉐𓏤2 𓅯𓄿 𓆱:𓏏*𓏤𓆱:𓏥𓊡𓏭:𓏛 𓅯𓄿𓏭1 𓂋1 𓂭:𓎆⸢𓆽𓍪⸣
|rto.x+II.16 𓅯𓄿 𓍓@𓉐𓏤2 𓉔1:𓈖1𓏌 𓈗𓏤1𓈘:𓈇 𓈖:𓏏*𓏭1 𓈝𓂻:° 𓂋1 𓏏:𓄿 𓎼𓃭𓉻:𓂝*𓏛𓀁° 𓈔𓏤𓈒:𓏥2 ⸢𓈖:𓏏*𓏭1 𓈝⸣[𓂻:°] ⸢𓂋1⸣ [𓅯𓄿] 𓆱:𓏏*𓏤𓆱:𓏥𓊡𓏭:𓏛
|rto.x+II.17 𓏲:𓏏𓏤𓋴𓏏@ 𓅯𓄿𓇋𓇋𓆑 𓋴𓅓:𓂧1 □
𓏺:
✓
:
𓏼1 𓍢 𓂋1 𓉔1:𓈖1𓏌 𓈗𓏤1𓈘:𓈇 𓂭:𓎆𓆽𓍪
|rto.x+II.18 𓌡:𓂝*𓏤3 𓆱:𓏏*𓏤𓆱:𓏥𓊡𓏭:𓏛 𓇋𓏲𓆑 𓊢𓂝:𓂻 𓇋𓏲𓆑 𓁹:𓂋*𓏭 𓅓1𓎔1𓊹𓅆 𓎎 𓅓1𓂸:𓏏𓂭𓂭⸢𓀁⸣ 𓇋𓏲𓆑 𓁹:𓂋*𓏭 𓅓1𓎔1𓊹𓅆 𓏼1 𓆷1𓃭𓏤𓀁 𓂋:𓂧@𓂾:°𓂾:°[𓍘1] 𓆑1 𓇋𓏲𓆑 [𓁹:𓂋*𓏭] ⸢𓅓1𓎔1⸣𓊹𓅆 𓏺 𓈖 𓄂:𓏏*𓏤𓄣𓏤𓄹:𓏭2@𓍘1 𓆑1
|rto.x+II.19 𓎼𓃭𓉻:𓂝*𓏛𓀁°𓏪 𓈔𓏤𓈒:𓏥2𓈔? 𓇋𓏲𓆑 𓄖:𓂻 𓇋𓏲𓏪 𓏎:𓈖 𓅯𓄿 𓆱:𓏏*𓏤⸢𓆱:𓏥⸣𓊡𓏭:𓏛 𓂋1𓈐:𓂻 𓏌:𓈖𓉐𓏤2 𓏏:𓄿 𓎼⸢𓃭⸣[𓉻:𓂝*𓏛]⸢𓀁 𓅓1𓏲:𓏏:°⸣ 𓏪 ⸢𓆼𓇋𓇋𓏲⸣𓂷:𓂡 𓈗⸢𓏤1𓈘:𓈇⸣
|rto.x+II.20 𓇋𓋴𓏏 𓂷:𓂡1 𓇋1𓐍:𓏭 𓈗𓏤1𓈘:𓈇 𓇋1𓐍:𓏭 𓅯𓄿 𓍓@𓉐𓏤2 𓉔1:𓈖1𓏤1𓈘:𓈇 𓈗𓏤1𓈘:𓈇 𓈖:𓏏*𓏭1𓇋𓏲 𓏏:𓄿 𓎼𓃭𓉻:𓂝*𓏛⸢𓀁⸣ 𓊏𓏲𓏭:𓏛
|rto.x+II.21 𓇋1𓐍:𓏭 𓅯𓄿 𓍓@𓉐𓏤2 𓅓1𓎔1𓊹𓅆 𓅯𓄿 𓆱:𓏏*𓏤𓆱:𓏥𓊡𓏭:𓏛 𓂽 𓅯𓄿 𓎼:𓂋𓇋𓇋𓏲𓀾° 𓈖2:
𓁹:𓂋*𓏭𓆑 𓏴:𓏛
|rto.x+II.22 𓇋5:𓎡 𓎝𓎛𓎛3 𓌡:𓂝*𓏤3 𓁷𓏤𓏤1 𓆷1𓃭𓏤𓀁 𓈖 𓄂:𓏏*𓏤𓄣𓏤𓄹:𓏭2@𓍘1 𓆑1 𓂋1 𓏼1 𓁷𓏤𓏤1 𓆷1𓃭𓏤𓀁 𓈖 𓂋:𓂧@𓂾:°𓂾:°𓍘1 𓆑1 𓂋1 ⸢𓏽1 𓇋5:𓎡⸣ 𓂷:𓂡1 𓅯𓄿𓇋𓇋𓆑 𓐝 𓂋1 𓏻1 𓇋5:𓎡 𓁹:𓂋*𓏭 𓏻1 𓂋1 𓊃2:𓊪1° ⸢𓏻1⸣ ↑
𓂋1 𓏽1↑
|rto.x+II.23 𓇋5:𓎡 𓂷:𓂡1 𓅯𓄿𓇋𓇋𓆑 𓏴 𓆣:𓂋𓏲 𓇋𓏲 𓈖:𓏏*𓏭1𓎟:𓏏 𓁷𓏤𓏤1 𓆷1𓃭𓏤𓀁° 𓐍':𓂋5𓀁° 𓌪:𓂡𓍘1 𓅯𓄿𓏲𓏛:𓏥 𓏴 𓈖𓇋𓅓𓏭:𓏛 𓏪 𓏭:𓂢 𓏼1
|rto.x+II.24 𓇋5:𓎡 𓁹:𓂋*𓏭 𓎎 𓂋1 𓊃2:𓊪1° 𓏼1 𓂋𓌥𓏲𓏭:𓏛 𓅯𓄿 𓅓1𓂸:𓏏𓂭𓂭𓀁° 𓅯𓄿 𓆱:𓏏*𓏤𓆱:𓏥𓊡𓏭:𓏛 𓈖:𓏏*𓏭1 𓁹:𓂋*𓏭 𓎎 𓂋1 𓍣𓎌 𓅯𓄿 𓍓@𓉐𓏤2 𓅯𓄿 𓆱:𓏏*𓏤𓆱:𓏥𓊡𓏭:𓏛 𓅯𓄿𓏭1
|rto.x+II.25 𓅯𓄿 𓎼:𓂋𓇋𓇋𓏲𓀾° 𓈖2:
𓅠𓏭:𓏛 𓅯𓄿 𓍓@𓉐𓏤2 𓉔1':𓈖1𓏤1𓈘:𓈇𓏤1𓈘:𓈇 𓈖:𓏏*𓏭1 𓈝𓂻:° 𓂋1 𓅯𓄿 𓅓1𓎔1 𓏺 𓁷𓏤𓏤1𓄡:𓏏*𓏤@ 𓏺 𓅓1𓏏1:𓇋𓇋𓏲𓀁° 𓆑 𓏺
|rto.x+II.26 𓇋5:𓎡 𓂋:𓐍@ 𓅯𓄿 𓍓@𓉐𓏤2 𓂧:𓏏*𓏤1 𓈖:𓏏*𓏭1 𓈝𓂻:° 𓂋1 𓅯𓄿 ⸢𓅓1𓎔1⸣𓅝:𓏏*𓏭𓅆° 𓂋1 𓐀1 𓇋5:𓎡 𓁹:𓂋*𓏭 𓐀 ⸢𓂋1⸣ 𓊃2:𓊪1° 𓐀 𓂋1 𓎉𓐂1
|rto.x+II.27 𓇋5:𓎡 𓁹:𓂋*𓏭 𓎉𓐂1 𓂋1 𓊃2:𓊪1° 𓐀 □
𓂋1 𓍤𓎉𓏼1 𓇋5:𓎡 𓆓:𓂧 𓅯𓄿 𓉔1:𓈖1𓏤1𓈘:𓈇 𓂧:𓏏*𓏤1 𓏺 𓁷𓏤𓏤1𓄡:𓏏*𓏤@ 𓏺 𓅓1𓏏1:𓇋𓇋𓏲𓀁 𓆑 ⸢𓏺⸣
|rto.x+II.28 𓇋5:𓎡 𓆓:𓂧 𓐍':𓂋5𓀁 𓈝𓂻:° 𓉔1:𓈖1𓏤1𓈘:𓈇 𓍤𓎉𓏼1 𓂋1 𓅓1𓎔1 𓏺 𓁷𓏤𓏤1𓄡:𓏏*𓏤 𓏺 𓅓1𓏏1:𓇋𓇋𓏲𓀁 𓆑 𓏺
|rto.x+II.29 𓇋5:𓎡 𓁹:𓂋*𓏭 𓍤𓎉𓏼1 𓂋1 𓊃2:𓊪1° 𓍣𓎌 𓈖:𓏏*𓏭1𓇋𓏲 𓁹:𓂋*𓏭 𓍓@𓉐𓏤2 𓅯𓄿 𓆱:𓏏*𓏤𓆱:𓏥𓊡𓏭:𓏛 𓂋1 𓂭:𓐂1𓆽𓍧⸢𓎆⸣
|rto.x+II.30 𓅯𓄿 𓍓@𓉐𓏤2 𓉔1:𓈖1𓏤1𓈘:𓈇 𓈖:𓏏*𓏭1 𓈝𓂻:° 𓂋1 𓏏:𓄿 𓎼𓃭[𓉻:𓂝*𓏛𓀁° 𓈔𓏤𓈒:𓏥2 𓈖:𓏏*𓏭1] ⸢𓈝⸣[𓂻:° 𓂋1] ⸢𓅯𓄿 𓆱:𓏏*𓏤𓆱:𓏥𓊡⸣[𓏭:𓏛 □
𓏲:𓏏𓏤𓋴𓏏@ 𓅯𓄿𓇋𓇋𓆑 𓋴]⸢𓅓:𓂧1𓀁1⸣ 𓏺:
✓
:
𓏼1 𓎎
|vso.x+IV.1 𓇋𓏲𓏪 𓆓:𓂧 𓈖2:𓎡 𓐁@ 𓈖 𓎝𓎛𓎛3 𓇋1𓐍:𓏭° 𓌪:𓂡𓍘1 𓅯𓄿𓏭1
|vso.x+IV.2 𓅯𓄿 𓎼:°𓇋𓇋𓏲𓀾° 𓈖2:
𓁹:𓂋*𓏭𓆑 𓏴:𓏛
|vso.x+IV.3 𓇋5:𓎡 𓎝𓎛𓎛3 𓐁@ 𓂋1 𓏺 □
𓂋1 𓏺 𓐁@
|vso.x+IV.4 𓇋5:𓎡 𓆓:𓂧 𓐁@ 𓅯𓄿 𓇋1𓐍:𓏭 𓐁@ 𓅯𓄿𓏭1 𓂋1 𓅯𓄿𓇋𓇋𓆑 𓐂1@
|vso.x+IV.5 𓇋5:𓎡 𓆓:𓂧 𓐁@ 𓈖 𓎝𓎛𓎛3 𓐂1@ 𓈖 𓌪:𓂡𓍘1
|vso.x+IV.6 𓂋1 𓂞:𓏏 ⸢𓁹:𓂋*𓏭⸣𓂋:𓐍:
𓎡1 𓋴𓏏@ 𓏴:𓏛
|vso.x+IV.7 𓇋5:𓎡 𓌪:𓂡𓍘1 𓐂1@ 𓏌:𓈖𓉐𓏤2 𓏺 𓏭:𓂢 [𓂌𓂋:𓏿2] 𓎈@ 𓎉⸢𓏾⸣
|vso.x+IV.8 𓅯𓄿 𓍓@𓉐𓏤2 𓂌𓂋:𓏿2 𓎈@ 𓎉𓏾 𓏴:𓏛
|vso.x+IV.9 𓅯𓄿𓇋𓇋𓆑 𓐁@ □
𓐂1@ 𓇋5:𓎡 𓎝𓎛𓎛3 𓆑 𓂋1𓂋:𓆑 𓂋1 𓏺 𓂽
|vso.x+IV.10 𓇋𓏲𓏪 𓆓:𓂧 𓈖2:𓎡 𓐂1@ 𓈖 𓎝𓎛𓎛3 𓇋1𓐍:𓏭 ⸢𓌪:𓂡⸣𓍘1 ⸢𓅯𓄿𓏭⸣
|vso.x+IV.11 𓅯𓄿 𓎼:°⸢𓇋𓇋𓏲⸣𓀾° 𓈖2:
𓁹:𓂋*𓏭𓆑 𓏴:𓏛
|vso.x+IV.12 𓇋5:𓎡 𓎝𓎛𓎛3 𓐂1@ [𓂋1 𓏺] □
𓂋1 𓏺 ⸢𓐂1@⸣
|vso.x+IV.13 𓇋5:𓎡 𓆓:𓂧 𓐂1@ 𓅯𓄿 𓇋1𓐍:𓏭 𓏺 𓐂1@ 𓅯𓄿𓏭1 𓂋1 𓅯𓄿𓇋𓇋𓆑 𓎆@
|vso.x+IV.14 𓇋5:𓎡 𓆓:𓂧 𓐂1@ 𓈖 𓎝𓎛𓎛3 𓎆@ 𓌪:𓂡𓍘1 𓅯𓄿𓏭1
|vso.x+IV.15 𓂋1 𓂞:𓏏 𓁹:𓂋*𓏭𓂋:𓐍:
𓎡1 ⸢𓋴𓏏@⸣ 𓏴:𓏛
|vso.x+IV.16 𓇋5:𓎡 𓌪:𓂡𓍘1 𓎆@ 𓏌:𓈖⸢𓉐𓏤2⸣ 𓏭:𓂢 𓂌𓂋:𓏿2 𓎆@[𓏾]
|vso.x+IV.17 𓅯𓄿 𓍓@𓉐𓏤2 𓂌𓂋:𓏿2 𓎆@𓏾 𓏴:𓏛
|vso.x+IV.18 𓅯𓄿𓇋𓇋𓆑 𓐂1@ □
𓎆@ 𓇋5:𓎡 𓎝𓎛𓎛3 𓆑 𓂋1𓂋:𓆑 𓂋1 𓏺 𓂽 (rto, x+II.1) wꜥ ḫt-ṯꜣw ỉw⸗f ⸢ꜥḥꜥ ḥr⸣ [pꜣ] .yꜣ(?).[. ỉw⸗f] ỉri̯ mḥ-(ꜥ-)nṯr 100 (n) mtỉ ỉw⸗f ỉri̯ mḥ-(ꜥ-)nṯr 3 (n) šl (n) rṱ⸗f (rto, x+II.2) ỉw⸗f ỉri̯ mḥ-(ꜥ-)nṯr 1 n ḥꜣṱ⸗f grꜥ.w (n) ḥmt ỉw⸗f pḥ ỉw⸗w ỉni̯ pꜣ ḫt-ṯꜣw r-⸢bnr⸣ ẖn (rto, x+II.3) tꜣ grꜥ(.t) mtw⸗w ḫꜣy ⸢mw⸣ r tꜣ grꜥ(.t) ỉw<⸗s> (r) ṯꜣi̯ ỉh̭ mw ⸢ꜥn⸣ (rto, x+II.4) ỉh̭ pꜣ wḏꜣ (n) mḥ-(ꜥ-)-ḫd (n) pꜣ ḫt-ṯꜣw □ pꜣ gy n ỉri̯⸗f wp-st (rto, x+II.5) ỉw⸗k wꜣḥ wꜥ ḥr šl n ḥꜣ.⸢ṱ⸣⸗f r 3 ḥr šl (n) rdṱ[⸗f] ⸢r 4⸣ (rto, x+II.6) ỉw⸗k ṯꜣi̯ tꜣy⸗f pš(.t) r 2 ỉw⸗k ỉri̯ 2 r sp 2 r 4 (rto, x+II.7) ỉw⸗k ṯꜣi̯ pꜣy⸗f 1/4 ḫpr ỉw ntỉ-nb ḥr šl ḫr šꜥṱ pꜣy⸗w 1/4 n.ỉm⸗w sp 3 (rto, x+II.8) ỉw⸗k ỉri̯ 100 r sp 3 r-ḏbꜣ pꜣ mtỉ (n) pꜣ ḫt-ṯꜣw ntỉ ỉri̯ (mḥ-ꜥ-nṯr) 100 r 300 pꜣ wḏꜣ (n) pꜣ ḫt-⸢ṯꜣw⸣ [pꜣỉ] (rto, x+II.9) pꜣ gy n gmi̯ pꜣ wḏꜣ (n) hn ntỉ šm r pꜣ mḥ-sp-2 1 ḥr-ẖ.t 1 mty[⸗f 1] (rto, x+II.10) ỉw⸗k rḫ pꜣ wḏꜣ (n) šsp ntỉ šm r pꜣ mḥ-ḏḥw.tỉ r 7 (rto, x+II.11) ỉw⸗k ỉri̯ 7 r sp 7 r 49 (rto, x+II.12) ỉw⸗k ỉri̯ 49 r sp 7 □ r 343 (rto, x+II.13) ỉw⸗k ḏd pꜣ hn šsp 1 ⸢ḥr-⸣ẖ.t 1 mty⸗f 1 (rto, x+II.14) ỉw⸗k ḏd ḫr šm hn [343 r mḥ-(ꜥ-ḫd)] 1 [ḥr-ẖ.t 1 mty⸗f 1] (rto, x+II.15) [ỉw⸗k ỉri̯] 34[3] r sp 300 ntỉ.ỉw pꜣ wḏꜣ (mḥ-ꜥ-ḫd n) pꜣ ḫt-ṯꜣw pꜣỉ r 10⸢2900⸣ (rto, x+II.16) pꜣ wḏꜣ (n) hn mw ntỉ šm r tꜣ grꜥ(.t) ḥmt ⸢ntỉ šm r⸣ [pꜣ] ḫt-ṯꜣw (rto, x+II.17) tw⸗s pꜣy⸗f smt □ 1 | 3 100 r hn mw 102900
(rto, x+II.18) wꜥ ḫt-ṯꜣw ỉw⸗f ꜥḥꜥ ỉw⸗f ỉri̯ mḥ-(ꜥ-)nṯr 90 (n) mtỉ ỉw⸗f ỉri̯ mḥ-(ꜥ-)nṯr 3 (n) šl (n) r[ṱ]⸗f ỉw⸗f [ỉri̯] ⸢mḥ-⸣(ꜥ-)nṯr 1 n ḥꜣṱ⸗f (rto, x+II.19) grꜥ.w (n) ḥmt
ỉw⸗f pḥ ỉw⸗w ỉni̯ pꜣ ḫt-ṯꜣw r-bnr ẖn tꜣ g⸢r⸣[ꜥ](.t) ⸢mtw⸣⸗w ⸢ḫꜣy⸣ ⸢mw⸣ (rto, x+II.20) ỉw⸗s (r) ṯꜣi̯ ỉh̭ mw ỉh̭ pꜣ wḏꜣ (n) hn (n) mw ntỉ.ỉw tꜣ grꜥ(.t) (r) šsp (rto, x+II.21) ỉh̭ pꜣ wḏꜣ (n) mḥ-(ꜥ-)-nṯr (n) pꜣ ḫt-ṯꜣw ꜥn pꜣ gy n ỉri̯⸗f wp-st (rto, x+II.22) ỉw⸗k wꜣḥ wꜥ ḥr šl n ḥꜣ.ṱ⸗f r 3 ḥr šl n rdṱ⸗f r ⸢4 (rto, x+II.6) ỉw⸗k⸣ ṯꜣi̯ pꜣy⸗f 1/2 r 2 ỉw⸗k ỉri̯ 2 r sp ⸢2⸣ ↑r 4↑ (rto, x+II.23) ỉw⸗k ṯꜣi̯ pꜣy⸗f 1/4 ḫpr ỉw ntỉ-nb ḥr šl ḫr šꜥṱ pꜣy⸗w 1/4 n.ỉm⸗w sp 3 (rto, x+II.24) ỉw⸗k ỉri̯ 90 r sp 3 r-ḏbꜣ pꜣ mtỉ (n) pꜣ ḫt-ṯꜣw ntỉ ỉri̯ (mḥ-ꜥ-nṯr) 90 r 270 pꜣ wḏꜣ (n mḥ-ꜥ-ḫd) pꜣ ḫt-ṯꜣw pꜣỉ (rto, x+II.25) pꜣ gy n gmi̯ pꜣ wḏꜣ (n) hn ntỉ šm r pꜣ mḥ(-ꜥ) 1 ḥr-ẖ.t 1 mty⸗f 1 (rto, x+II.26) ỉw⸗k rḫ pꜣ wḏꜣ (n) šsp ntỉ šm r pꜣ ⸢mḥ-⸣ḏḥw.tỉ r 7 ỉw⸗k ỉri̯ 7 ⸢r⸣ sp 7 r 49 (rto, x+II.27) ỉw⸗k ỉri̯ 49 r sp 7 □ r 343 ỉw⸗k ḏd pꜣ hn šsp 1 ḥr-ẖ.t 1 mty⸗f ⸢1⸣ (rto, x+II.28) ỉw⸗k ḏd ḫr šm hn 343 r mḥ-(ꜥ-ḫd) 1 ḥr-ẖ.t 1 mty⸗f 1 (rto, x+II.29) ỉw⸗k ỉri̯ 343 r sp 270 ntỉ.ỉw ỉri̯ wḏꜣ (mḥ-ꜥ-ḫd n) pꜣ ḫt-ṯꜣw r 926⸢10⸣ (rto, x+II.30) pꜣ wḏꜣ (n) hn ntỉ šm r tꜣ gr[ꜥ(.t) ḥmt ntỉ] ⸢šm⸣ [r] ⸢pꜣ ḫt-ṯꜣw⸣ □ [tw⸗s pꜣy⸗f s]⸢mt⸣ □ 1 | 3 90
(vso, x+IV.1) ỉw⸗w ḏd n⸗k 1/8 n wꜣḥ ỉh̭ šꜥṱ pꜣỉ (vso, x+IV.2) pꜣ gy n ỉri̯⸗f wp-st (vso, x+IV.3) ỉw⸗k wꜣḥ 1/8 r 1 □ r 1 1/8 (vso, x+IV.4) ỉw⸗k ḏd 1/8 pꜣ ỉh̭ (n) <1> 1/8 pꜣỉ r pꜣy⸗f 1/9 (vso, x+IV.5) ỉw⸗k ḏd 1/8 n wꜣḥ 1/9 n šꜥṱ (vso, x+IV.6) r ḏi̯.t ⸢ỉri̯.⸣rḫ⸗k s wp-st (vso, x+IV.7) ỉw⸗k šꜥṱ 1/9 ẖn 1 sp [5/6] 1/30 1/4⸢5⸣ (vso, x+IV.8) pꜣ wḏꜣ 5/6 1/30 1/45 wp-st (vso, x+IV.9) pꜣy⸗f 1/8 □ 1/9 ỉw⸗k wꜣḥ⸗f r.r⸗f r 1 ꜥn
(vso, x+IV.10) ỉw⸗w ḏd n⸗k 1/9 n wꜣḥ ỉh̭ ⸢šꜥ⸣ṱ ⸢pꜣỉ⸣ (vso, x+IV.11) pꜣ g⸢y⸣ n ỉri̯⸗f wp-st (vso, x+IV.12) ỉw⸗k wꜣḥ 1/9 [r 1] □ r 1 ⸢1/9⸣ (vso, x+IV.13) ỉw⸗k ḏd 1/9 pꜣ ỉh̭ (n) 1 1/9 pꜣỉ r pꜣy⸗f 1/10 (vso, x+IV.14) ỉw⸗k ḏd 1/9 n wꜣḥ 1/10 (n) šꜥṱ pꜣỉ (vso, x+IV.15) r ḏi̯.t ỉri̯.rḫ⸗k ⸢s⸣ wp-st (vso, x+IV.16) ỉw⸗k šꜥṱ 1/10 ẖn <1> sp 5/6 1/1[5] (vso, x+IV.17) pꜣ wḏꜣ 5/6 1/15 wp-st (vso, x+IV.18) pꜣy⸗f 1/9 □ 1/10 ỉw⸗k wꜣḥ⸗f r.r⸗f r 1 ꜥn
(rto, x+II.1) Ein Mast, der auf [dem/der] ... steht, indem er 100 Gottesellen an Länge ausmacht, indem er 3 Gottesellen an Durchmesser an seinem Fuß ausmacht, (rto, x+II.2) (und) indem er 1 Gotteselle (an Durchmesser) an seiner Spitze ausmacht, ist in Kupfer eingefasst. Wenn es eintrifft, dass der Mast aus (rto, x+II.3) der Einfassung (rto, x+II.2) geholt wird (rto, x+II.3) und Wasser in die Einfassung abgemessen wird, wieviel Wasser wird sie wiederum aufnehmen? (rto, x+II.4) Was ist die Anzahl an Quadratellen des Mastes? □ Die Art es zu tun; im Einzelnen: (rto, x+II.5) Du sollst Eins für den Durchmesser seiner Spitze zu 3 für den Durchmesser [seines] Fußes addieren, macht 4. (rto, x+II.6) Du sollst seine Hälfte nehmen, macht 2. Du sollst 2 mal 2 rechnen, macht 4. (rto, x+II.7) Du sollst sein 1/4 nehmen, was(?) auch(?) immer(?) dem Durchmesser passiert; dann subtrahiere ihr 1/4 von ihnen, Rest: 3. (rto, x+II.8) Du sollst 100 mal 3 rechnen wegen der Länge des Mastes, die 100 (Gottesellen) ausmacht, macht 300. Das ist die Anzahl (an Quadratellen) des Mastes.
(rto, x+II.9) Die Art, die Anzahl an Hin zu finden, die in die wirkliche Elle gehen, 1 mal 1, [ihre] Tiefe ist [1]: (rto, x+II.10) Du kennst die Anzahl an Handbreiten, die in die Elle des Thot gehen, macht 7. (rto, x+II.11) Du sollst 7 mal 7 rechnen, macht 49. (rto, x+II.12) Du sollst 49 mal 7 rechnen, □ macht 343. (rto, x+II.13) Du sollst sagen: "Das Hin ist 1 Handbreite mal 1, seine Tiefe ist 1.". (rto, x+II.14) Du sollst sagen: "[343] Hin gehen [in eine (Quadrat)elle,] 1 [mal 1, ihre Tiefe ist 1."]. (rto, x+II.15) [Du sollst] 34[3] mal 300 [rechnen], was die Anzahl (an Quadratellen) des Mastes ist, macht 102900, (rto, x+II.16) die Anzahl an Hin von Wasser, die in die Einfassung aus Kupfer gehen (und) die in [den] Mast gehen. (rto, x+II.17) Siehe, sein Plan: □ 1 | 3 100, macht 102900 Hin von Wasser.
(rto, x+II.18) Ein Mast, der steht, indem er 90 Gottesellen an Länge ausmacht, indem er 3 Gottesellen an Durchmesser an seinem Fu[ß] ausmacht, (und) indem er 1 Gotteselle (an Durchmesser) an seiner Spitze [ausmacht], (rto, x+II.19) ist in Kupfer eingefasst. Wenn es eintrifft, dass der Mast aus der Einfass[ung] geholt wird und Wasser abgemessen wird, (rto, x+II.20) wieviel Wasser wird sie aufnehmen? Was ist die Anzahl an Hin von Wasser, die die Einfassung aufnehmen wird? (rto, x+II.21) Was ist wiederum die Anzahl an Gottesellen des Mastes? Die Art es zu tun; im Einzelnen: (rto, x+II.22) Du sollst Eins für den Durchmesser seiner Spitze zu 3 für den Durchmesser seines Fußes addieren, macht 4. (rto, x+II.6) Du sollst sein 1/2 nehmen, macht 2. Du sollst 2 mal 2 rechnen, ↑macht 4↑. (rto, x+II.23) Du sollst sein 1/4 nehmen, was(?) auch(?) immer(?) dem Durchmesser passiert; dann subtrahiere ihr 1/4 von ihnen, Rest: 3. (rto, x+II.24) Du sollst 90 mal 3 rechnen wegen der Länge des Mastes, die 90 (Gottesellen) ausmacht, macht 270. Das ist die Anzahl (der Quadratellen) des Mastes. (rto, x+II.25) Die Art, die Anzahl an Hin zu finden, die in die Elle gehen, 1 mal 1, ihre Tiefe ist 1: (rto, x+II.26) Du kennst die Anzahl an Handbreiten, die in die Elle des Thot gehen, macht 7. Du sollst 7 mal 7 rechnen, macht 49. (rto, x+II.27) Du sollst 49 mal 7 rechnen, □ macht 343. Du sollst sagen: "Das Hin ist 1 Handbreite mal 1, seine Tiefe ist 1.". (rto, x+II.28) Du sollst sagen: "343 Hin gehen in eine (Quadrat)elle, 1 mal 1, ihre Tiefe ist 1.". (rto, x+II.29) Du sollst 343 mal 270 rechnen, was die Anzahl (an Quadratellen) des Mastes ausmacht, macht 92610, (rto, x+II.30) die Anzahl an Hin von Wasser, die in die Einfassung aus Kupfer gehen (und) die in [den] Mast gehen. □ [Siehe, sein P]lan: □ 1 | 3 90
(vso, x+IV.1) Wenn zu dir gesagt wird: "Ein Plus von 1/8 - was ist der Anteil (an der Gesamtsumme)?". (vso, x+IV.2) Die Art es zu tun; im Einzelnen: (vso, x+IV.3) Du sollst 1/8 zu 1 addieren, □ macht 1 1/8. (vso, x+IV.4) Du sollst sagen: "Was ist 1/8 von <1> 1/8?", macht sein 1/9. (vso, x+IV.5) Du sollst sagen: "1/8 ist das Plus, 1/9 ist der Anteil (an der Gesamtsumme)". (vso, x+IV.6) Um es dich überprüfen zu lassen; im Einzelnen: (vso, x+IV.7) Du sollst 1/9 von 1 abziehen; Rest: [5/6] 1/30 1/45. (vso, x+IV.8) Die Zahl 5/6 1/30 1/45 im Einzelnen: (vso, x+IV.9) Ihr 1/8 (ist) □ 1/9. Du sollst es (das 1/9) zu ihr (den 5/6 1/30 1/45) addieren, macht wieder 1.
(vso, x+IV.10) Wenn zu dir gesagt wird: "Ein Plus von 1/9 - was ist der Anteil (an der Gesamtsumme)?". (vso, x+IV.11) Die Art es zu tun; im Einzelnen: (vso, x+IV.12) Du sollst 1/9 [zu 1] addieren, □ macht 1 1/9. (vso, x+IV.13) Du sollst sagen: "Was ist 1/9 von 1 1/9?", macht sein 1/10. (vso, x+IV.14) Du sollst sagen: "1/9 ist das Plus, 1/10 ist der Anteil (an der Gesamtsumme)". (vso, x+IV.15) Um es dich überprüfen zu lassen; im Einzelnen: (vso, x+IV.16) Du sollst 1/10 von <1> abziehen; Rest: 5/6 1/1[5]. (vso, x+IV.17) Die Zahl 5/6 1/15 im Einzelnen: (vso, x+IV.18) Ihr 1/9 (ist) □ 1/10. Du sollst es (das 1/10) zu ihr (den 5/6 1/15) addieren, macht wieder 1.
(29/11/2021)